|
|
|
|
-
-
-
Transition from first-order to zero-order kinetics is described by the Michaelis-Menten model of enzyme kinetics, which provides a mathematical description for saturable, capacity-limited elimination processes.
-
The elimination rate follows from the equation:
-
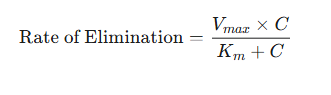
-
where:
-
Vmax is the maximum rate of the elimination process (e.g., mg/hr).
-
Km (the Michaelis constant) is the drug concentration at which the rate of elimination is exactly half of Vmax .
-
Km is a measure of the affinity of the enzymes for the drug; a low Km is suggestive of high affinity.
-
-
is the plasma drug concentration.
-
-
-
At low concentrations (C << Km ):
-
The concentration in the denominator is negligible compared to Km .
-
The equation simplifies to Rate ≈ ( Vmax / Km ) * .
-
Since Vmax and Km are constants, the rate is directly proportional to the concentration, which is the definition of first-order kinetics.
1
-
-
-
(C >> Km ): -
The Km-
Rate ≈. -
1
-
-
-
"Michaelis-Menten elimination kinetics: relationship of concentration and clearance rate" 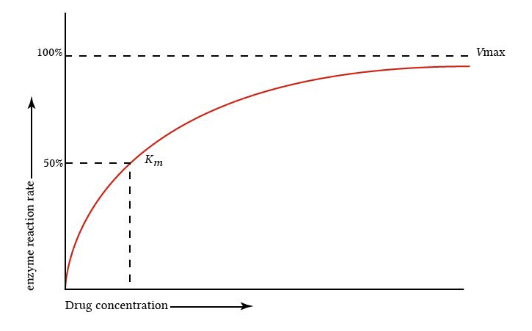
-
Attribution:
-
This figure is from "Michaelis-Menten elimination kinetics: relationship of Concentrationa clearance rate", describing Michaelis-Menten elimination kinetics.
-
Yartsev A First-order, zero-order and non-linear elimination kinetics. Deranged Physiology: Pharmacokinetics. (Last updated December 18, 2023): https://derangedphysiology.com/main/cicm-primary-exam/pharmacokinetics/Chapter-337/first-order-zero-order-and-non-linear-elimination-kinetics1
-
-
-
-
Clinical Implications of Michaelis-Menten Kinetics
-
Drugs that have a therapeutic range that falls on the steep, transitional part of the Michaelis-Menten curve are said to have a narrow therapeutic index and pose significant clinical challenges.
1,2 -
Phenytoin3, theophylline, and high-dose salicylates (aspirin) are examples.
-
-
-
-
-
Drug Accumulation and Steady-State Concentration (Css)
-
Most therapeutic drug regimens involve the administration of multiple doses of a drug over time.
-
Understanding how a drug behaves under these conditions is crucial for maintaining its concentration within the desired therapeutic range.
-
-
Principle of Accumulation
-
When a drug is administered repeatedly at a fixed dosing interval (τ) that is shorter than the time required for its complete elimination (approximately 4-5 half-lives), the drug will accumulate in the body.
-
5,6 -
7 -
-
-
-
-
Attainment of Steady State (Css)
-
With each successive dose, the peak (maximum) and trough (minimum) concentrations of the drug will rise until they reach a plateau.
-
This plateau is known as the steady-state concentration, (Css)
-
"Fundamental pharmacokinetic relationships for repeated administration of drugs" 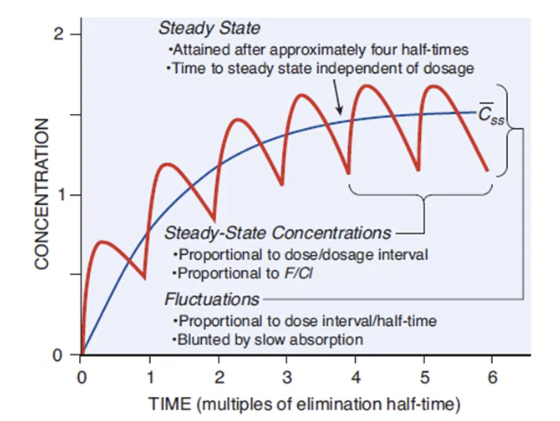
-
Attribution
-
Figure 1 from reference (6).
-
Exploring the Importance in Ways to Achieve Steady State in Pharmacokinetics. BioPharma Services Inc. https://www.biopharmaservices.com/blog/phase-1-exploring-the-importance-and-ways-to-achieve-steady-state-in-pharmacokinetics/
-
-
-
At steady state, a dynamic equilibrium is achieved where the amount of drug administered during a dosing interval is exactly equal to the amount of drug eliminated during that same interval.
-
The rate of drug administration equals the rate of drug elimination (Rate In = Rate Out).
-
Once steady state is reached, the plasma concentrations will fluctuate between a constant peak (Css,max) and a constant trough (Css,min) with each dosing interval, as long as the dose and interval remain unchanged.
-
-
A important concept in clinical practice is the time required to reach steady state.
-
This time is determined solely by the drug's elimination half-life (t1/2) and is independent of the size of the dose or the frequency of the dosing interval.
-
It takes approximately 4 to 5 half-lives for plasma concentrations to reach about 97% of their final steady-state value.8
-
-
-
-
Factors Influencing the Level of Css
-
While the time to reach steady state is dependent only on half-life, the level or magnitude of the steady-state concentration is determined by the balance between the dosing rate and the drug's clearance.
-
The average steady-state concentration, (Css,avg) is described by the following equation9:
-
Css,avg = F * D / CL * τ
-
Where
-
F is the bioavailability.
-
Dose is the amount of drug given per administration.
-
CL is the total body clearance.
-
-
-
-
-
-
-
τ
The equation illustrates that the steady-state concentration is directly proportional to the bioavailability and the dose, and inversely proportional to the clearance and the dosing interval.
-
This distinction between the factors controlling the time to reach steady state and the factors controlling the level of steady state is clinically important. The steady-state concentration may be altered by adjusting the dose or the dosing interval.
-
For example, doubling the maintenance dose will approximately double the eventual Css .
-
However, making this change will not make the patient reach that new, higher steady state any faster; it will still take 4 to 5 half-lives.
-
This principle is the fundamental reason why loading doses are necessary for drugs with very long half-lives such as for amiodarone with a t1/2 of over 50 days.
-
Without a loading dose, it would take months to achieve a therapeutic effect, which is likely clinically unacceptable.
-
-
-
-
Drug Accumulation Ratio (Rac)
-
The extent to which a drug accumulates can be quantified by the accumulation ratio (Rac).
-
This ratio compares the drug exposure at steady state to the exposure after a single dose.
-
An Rac of 1 indicated no accumulation.
-
It can be predicted using the elimination rate constant (k) and the dosing interval (τ).
-
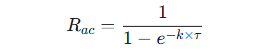
-
This equation shows that accumulation becomes more significant as the dosing interval, (τ) becomes shorter relative to the drug's half-life, since k = 0.693 / t1/2
-
This ratio is useful in both drug development and clinical practice for predicting the degree of accumulation with a proposed dosing regimen and assessing the potential risk of toxicity.
-
-
-
-
-
-
Bioavailability is the key pharmacokinetic parameter that quantifies this process, representing the bridge between the administered dose and the concentration of drug that the body's systems of distribution and elimination will act upon. This section introduces principles of bioavailability, consequences of first-pass elimination, and the relationship between bioavailability and the hepatic extraction ratio.
-
-
Principles of Bioavailability (F) -
n. -
F accounts for both rate and extent of absorption.10
-
-
Absolute vs. Relative Bioavailability11
-
Absolute bioavailability is the most fundamental measure.
-
Absolute bioavailability compares bioavailability of a drug administered via any non-intravenous route (e.g., oral, intramuscular, transdermal) to the bioavailability of the same drug given intravenously (IV).
-
Since an IV dose is administered directly into the systemic circulation, it is assumed to have 100% bioavailability, or F = 1 and provide the reference standard for comparisons.
-
-
Relative bioavailability is used to compare two different formulations of the same drug (e.g., a brand-name tablet versus a generic tablet, or a tablet versus a capsule).
-
This metric assesses whether the two formulations deliver the drug to the systemic circulation to the same extent and at the same rate Aand represents the basis of bioequivalence studies required for the approval of generic drugs.11
-
-
-
Assessing Bioavailability
-
The most reliable method for determining bioavailability involves comparing the total systemic exposure to the drug after different routes of administration.
-
Exposure to the drug is quantified by the area under the plasma concentration-time curve (AUC) which is directly proportional to the total amount of unchanged drug that reaches the systemic circulation.
-
Absolute Bioavailability11 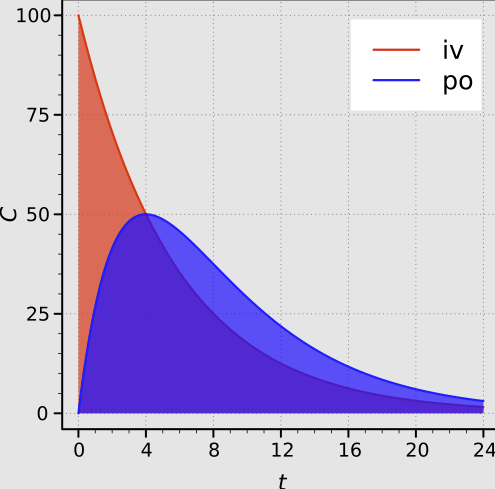
-
"Areas under the plasma concentration-time curves after intravenous and oral administration with complete absorption."
-
Attribution:
-
Alfie↑↓©, CC0, via Wikimedia Commons
-
-
-
-
The absolute bioavailability (F) of an oral formulation, for example, is calculated using the following dose-normalized equation:
-
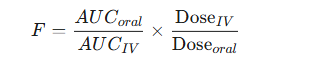
-
If the same dose is used for both oral and IV administration, the equation simplifies to the ratio of the AUCs.
-
-
-
-
-
-
Factors Affecting Bioavailability
-
Drug Properties: The intrinsic physicochemical properties of the drug are especially important.
-
These properties include:
-
Aqueous solubility (which affects dissolution)
-
Stability in the acidic environment of the stomach and enzymatic environment of the intestine,
-
Molecular size, and
-
pKa (which determines its ionization state and ability to cross lipid membranes)12
-
-
-
Dosage Form and Formulation: The design of the drug product can significantly impact bioavailability.
-
Factors include:
-
Use of different salt forms
-
Particle size of the drug (micronization can improve dissolution), and
-
Type and amount of inactive ingredients, or excipients, used in the formulation. (Excipients can influence the drug's dissolution rate and stability).12
-
-
-
Physiological and Patient-Specific Factors: The patient's individual physiology plays a major role.
-
Factors include:
-
pH of gastrointestinal fluids
-
Rate of gastric emptying and intestinal motility
-
Presence or absence of food (which can enhance, delay, or reduce absorption), and
-
Patient's age
-
Disease states such as malabsorption syndromes (e.g., Crohn's disease) or liver disease can also profoundly affect bioavailability.
-
Genetic variations in the expression of drug transporters in the gut wall (e.g., P-glycoprotein) can cause significant inter-individual differences in drug absorption.
12,13
-
-
-
-
-
-
-
First pass effect describes metabolism of a drug that occurs
14
-
-
-
-
-
The blood vessels draining the stomach and intestines do not lead directly to the general circulation; instead, they collect into the hepatic portal vein, which transports the blood directly to the liver.
-
This anatomical arrangement means that an orally absorbed drug must pass through two major sites of potential metabolism before reaching the systemic circulation.
-
-
The Gut Wall: The epithelial cells lining the intestine are metabolically active and contain a significant concentration of drug-metabolizing enzymes, particularly the cytochrome P450 isoform CYP3A4. A portion of the drug can be metabolized as it is being absorbed across the intestinal wall.14
-
The Liver: After passing through the gut wall and entering the portal circulation, the drug is delivered to the liver, which is the body's primary metabolic organ.
-
The liver can extensively metabolize the drug before it passes into the hepatic vein and enters the systemic circulation.14
-
-
-
Clinical Consequences of First-Pass Metabolism
-
The first-pass effect can dramatically reduce the oral bioavailability of a drug.
13 -
For drugs that are highly susceptible to first-pass metabolism, such as nitroglycerin, lidocaine, and propranolol, only a small fraction of the oral dose may reach the systemic circulation unchanged.
-
This first-pass effect sensitivity has several important clinical consequences.
-
Such drugs may require much larger oral doses compared to parenteral (e.g., IV or sublingual) doses to achieve the same therapeutic effect.
-
Some drugs are so extensively metabolized on the first pass that they are not effective when given orally and must be administered by an alternative route that bypasses the liver (e.g., sublingual nitroglycerin, IV lidocaine).
-
There can be large inter-individual variability in the extent of first-pass metabolism, leading to unpredictable plasma concentrations and responses after oral administration.
-
-
-
-
Hepatic Extraction Ratio (E) and its Impact on Bioavailability
-
The concept of the hepatic extraction ratio (E), introduced earlier in the context of hepatic clearance, is directly and intimately linked to bioavailability.
-
E represents the fraction of drug removed by the liver in a single pass.
-
Therefore, the fraction of drug that survives the first pass through the liver is simply (1 - E).
-
-
Applicable Equation
-
Assuming a drug is completely absorbed from the gastrointestinal tract (i.e., the fraction absorbed, fa, is 1), its oral bioavailability (F) is determined entirely by the fraction that escapes hepatic extraction. This relationship is expressed as: F = 1 - E.
-
If absorption from the gut is incomplete, the equation becomes F = fa * (1 - E).
-
This equation demonstrates that bioavailability is fundamentally limited by both the extent of absorption from the gut and the extent of first-pass elimination by the liver.
-
A high extraction ratio inevitably leads to low oral bioavailability.
-
-
-
Clinical Implications Based on Extraction Ratio15
-
High-Extraction Drugs (High E): These drugs, by definition, have a low oral bioavailability (F is low).
-
Their bioavailability is also highly sensitive to any changes in the liver's metabolic capacity or blood flow.
-
This circumstance results in significant inter-patient variability in plasma concentrations following oral administration, making such patients more challenging to dose predictably.
-
-
-
Their bioavailability is less affected by changes in liver function or blood flow but is more dependent on the extent of absorption from the gut
.
-
-
-
Consider a drug with a high extraction ratio of E = 0.9, resulting in an oral bioavailability of F = 10% (1 - 0.9).
-
If a patient takes a second drug that is a potent inhibitor of the relevant metabolic enzyme, it might reduce the liver's metabolic capacity and decrease the extraction ratio by a seemingly modest amount, for example, to E = 0.7.
-
The new bioavailability would be F = 30% (1 - 0.7).
-
In this scenario, a 22% reduction in the extraction ratio has resulted in a 200% (three-fold) increase in the amount of drug reaching the systemic circulation.
-
This amplification effect is why interactions involving enzyme inhibitors (such as certain antifungal drugs or even grapefruit juice) can lead to dramatic and dangerous increases in the plasma concentrations of co-administered high-extraction drugs.
-
The impact on bioavailability is often much greater than the impact on the clearance of the drug once it is already in the systemic circulation.
-
-
-
-
-
-
-
Summary of Key Pharmacokinetic Parameters and Governing Equations Parameter Symbol Conceptual Definition Primary Governing Equation Notes Volume of Distribution1 Vd The apparent volume into which the drug distributors to produce the observed plasma concentration. Vd = Amount of drug in body / plasma concentration Influenced by lipophilicity, protein binding, tissue binding, patient fluid status. Used to calculate loading dose. Loading Dose2 LD The initial dose given to rapidly achieve the target concentration. LD = Css * Vd) / F For IV administration, F=1. Css Is the target steady-state concentration Clearance3 CL The volume plasma cleared of drug per unit time. The most important parameter for maintenance dosing. CL = DoseIV/AUC OR CL = k * Vd CLT = CLr +CLh + CLother Hepatic Clearance4 CLh The volume of plasma cleared of drug per unit time by the liver. CLh = QH * E For high-E drugs, C≈ QH. For low-E drugs, CLh ≈ fu * CLint Renal Clearance5 CLr The volume of plasma cleared of drug per unit time by the kidneys. CLr = Rate of Renal Excretion / C Net result of filtration, secretion, and reabsorption. CLr = fe * CLT Elimination Half-Life6 t1/2 The time required for drug concentration to decreased by 50%. t1/2 = (0.693 * Vd )/ CL A dependent variable. Determines time to steady-state in dosing interval. Elimination Rate Constant7 k or kel The fraction of drug eliminated per unit time. k = CL / Vd The slope of the log-linear plasma concentration decline. k = 0.693 / t1/2 Bioavailability8 F The fraction of an administered dose that reaches systemic circulation. F=(AUCoral/AUCIV) * (DoseIV/Doseoral) For oral drugs, limited by absorption (fa) and first-pass effect: F = fa * (1-E) Extraction Ratio9 E The fraction of drug removed by an organ in a single pass. E = (CA - CV) / CA OR E = CLh / QH Inversely related to bioavailability. Classifies drugs as high- or low-extraction. Maintenance Dose Rate10 MD Rate The rate of drug administration required to maintain eight target steady-state concentration. MD Rate = Css * CL For oral dosing, Dose / τ = (Css * CL) / F Steady-State Concentration11 Css The plateau concentration where rate of administration equals rate of elimination. Css,avg = (F * Dose)/ CL * τ Reached in about 5 half-lives. Level is proportional to dose and inversely to clearance. Michaelis Menten Elimination12 Rate Describes saturable, capacity-limited elimination Rate= (Vmax * C) / Km + C Describes transition from first-order to zero-order kinetics. Important for drugs with narrow therapeutic windows.
References for Pharmacokinetic Equation Table
Mansoor A Mahabadi Volume of Distribution. StatPearls. National Library of Medicine Bookshelf. (Last update: July 24, 2023). https://www.ncbi.nlm.nih.gov/books/NBK545280/
Pharmacological principles: pharmacokinetic calculations: Pharmacological principles: https://ditki.com/course/usmle-comlex-high-yield/pharmacology/pharmacokinetic-principles/1634/pharmacokinetic-calculations/notes
Clearance & Area Under the Curve: Sketchy https://www.sketchy.com/medical-lessons/clearance-area-under-the-curve
Pharmacokinetics: online content for students. https://sepia2.unil.ch/pharmacology/parameters/hepaticclearance/
Pharmacokinetics V: What is Clearance?-Renal Clearance. https://www.abdn.ac.uk/medical/elf/courses/view/144053/pharmacokinetics-v/1/page9
Haollare J Gerriets Elimination Half-lLfe of Drugs: StatPearls. National Library of Medicine Bookshelf. (Last updated: May 3, 2025). https://www.ncbi.nlm.nih.gov/books/NBK554498/
Useful Pharmacokinetic Equations: https://pharmacy.ufl.edu/files/2013/01/5127-28-equations.pdf
Price G Patel D Drug Bioavailability. StatPearls. National Library of Medicine Bookshelf. (Last update July 30, 2023). https://www.ncbi.nlm.nih.gov/books/NBK557852/
Pharmacokinetics: Online content for students.: Extraction Ratio. https://sepia2.unil.ch/pharmacology/parameters/extractionratio/
Birkett DJ Pharmacokinetics made easy 11 Designing dose regimens. Australian Prescriber. 1996;19: 76-78. https://australianprescriber.tg.org.au/articles/pharmacokinetics-made-easy-11-designing-dose-regimens.html
Understanding Steady State Pharmacokinetics. Certara. https://www.certara.com/knowledge-base/understanding-steady-state-pharmacokinetics/
Michaelis-Menten Equation: Biopharmaceutics and Pharmacokinetics: Nonlinear Pharmacokinetics. Pharmacy180.com https://www.pharmacy180.com/article/michaelis-menten-equation-2530/
|
|
References
Tamargo J Le Heuzey J_Y Mabo P Narrow therapeutic index drugs: eight clinical pharmacological consideration to flecanide. Eur J Clin Pharmacol. 2015 April 15;71(5): 549-567. https://pmc.ncbi.nlm.nih.gov/articles/PMC4412688/ Sumarno Kusumastuti K Khotib J An analysis of the Michaelis-Menten pharmacokinetics of phenytoin epileptic Indonesian adults. Pharmacy Education (2023) 23(4) 311-315. https://www.researchgate.net/publication/374614433_An_analysis_of_the_Michaelis-Menten_pharmacokinetics_of_phenytoin_in_epileptic_Indonesian_adults Tsuchiya T Levy G Relationship between Dose and Plateau Levels of Drugs Eliminated by Parallel First-Order and Capacity-Limited Kinetics. Journal of Pharmaceutical Sciences. Volume 61, Issue 4, April 1972 541-544. https://www.sciencedirect.com/science/article/abs/pii/S0022354915384185 Exploring the Importance in Ways to Achieve Steady State in Pharmacokinetics. BioPharma Services Inc. https://www.biopharmaservices.com/blog/phase-1-exploring-the-importance-and-ways-to-achieve-steady-state-in-pharmacokinetics/ Henry A Accumulation: What It Means and How to Calculate It. Certara. https://www.certara.com/knowledge-base/accumulation-what-it-means-and-how-to-calculate-it/ (Originally published November 2012 and subsequently updated for accuracy) Pharmacokinetic Considerations for Repeat-Dosing. Allucent. https://www.allucent.com/resources/blog/pharmacokinetic-considerations-repeat-dosing Hallare J Gerriets Elimination Half-Life of Drugs. StatPearls. National Library of Medicine Bookshelf. (Last update May 3, 2025). https://www.ncbi.nlm.nih.gov/books/NBK554498/ Useful Pharmacokinetic Equations: https://pharmacy.ufl.edu/files/2013/01/5127-28-equations.pdf Grogan S Preuss C Pharmacokinetics. StatPearls. National Library of Medicine Bookshelf. (Last update: July 30, 2023). https://www.ncbi.nlm.nih.gov/books/NBK557744/ Bioavailability. https://en.wikipedia.org/wiki/Bioavailability Le J Drug Bioavailability. Pharmacokinetics: Drug Bioavailability. Merck manual Professional Version. (Review/revised November 2024). https://www.merckmanuals.com/professional/clinical-pharmacology/pharmacokinetics/drug-bioavailability Price G Patel D Drug Bioavailability. StatPearls. National Library of Medicine Bookshelf. (Last update July 30, 2023). https://www.ncbi.nlm.nih.gov/books/NBK557852/ First pass effect. https://en.wikipedia.org/wiki/First_pass_effect Yartsev A Hepatic Clearance. Deranged Physiology: Pharmacokinetics (last updated December 18, 2023): https://derangedphysiology.com/main/cicm-primary-exam/pharmacokinetics/Chapter-3336/hepatic-clearance |