Clinical Pharmacokinetics

• Basic and Applied Pharmacokinetics:  Audio Overview (2025)

• Introduction

  • Pharmacokinetics in Therapeutics

    • Pharmacokinetics (PK) is the scientific discipline dedicated to the quantitative study of the time course of a drug's absorption, distribution, metabolism, and excretion (ADME) within a living organism.

      • Pharmacokinetics describes what the body does to a drug, a process that stands in contrast to pharmacodynamics (PD), which considers the drug does to the body.

      • The purpose of clinical pharmacokinetics is to provide a rational, scientific basis for the therapeutic management of drugs in individual patients.

        • By describing relationships between drug concentrations in accessible fluids like plasma and the subsequent pharmacological responses, pharmacokinetic analysis promotes enhancement of therapeutic efficacy while limiting drug toxicity.

          • This expectation depends on on assumption that the concentration of a drug in the plasma is proportional to its concentration at the site of action, such as receptors in the CNS or on cardiac muscle.

    • Understanding the principles of pharmacokinetics is important in medicine because knowing the pharmacokinetic characteristic of the drug allows prescribers to base dosing on both drug characteristics and the patient's physiological state.

      • Variability in how individuals handle drugs—due to genetics, disease states like renal or hepatic insufficiency, age, or drug interactions—can lead to significant differences in plasma concentrations from a given dose, resulting in either therapeutic failure or adverse events.

      • Pharmacokinetics provides the mathematical framework to anticipate and manage this variability

    • This section provides an introduction to core principles of clinical pharmacokinetics.

      • Firstly, drug disposition with respect to both the drug's volume of distribution, the extent to which a drug is distributed throughout the body and the drug half-life, which quantifies its persistence.

      • Secondly, The report considers the concept of drug clearance, the body's efficiency in eliminating a drug, emphasizing roles of  liver and kidneys.

      • Thirdly, non-linear behavior of capacity-limited elimination and the principles of drug accumulation upon repeated dosing are introduced.

      • Lastly, bioavailability, which determines how much drug enters the systemic circulation  and pharmacokinetic equations that form the quantitative basis of drug therapy are discussed.

• Drug Disposition

   

  • Absorption, Distribution, Metabolism, and Excretion (ADME)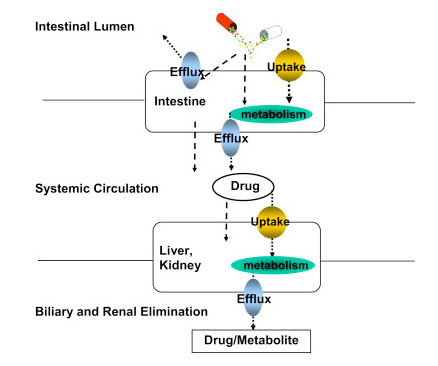

    "Schematic of drug uptake and efflux transporters, and metabolizing enzyme expression organs such as the intestine and liver that governs drug absorption, distribution, metabolism, and excretion (ADME)." Attribution: Tirona R Kim R Clinical and Translational Science, 2e , 2017 : Introduction: Mechanisms of Drug Disposition and Interactions. https://www.sciencedirect.com/topics/biochemistry-genetics-and-molecular-biology/drug-disposition

  • The behavior of the drug in the body is defined by two independent pharmacokinetic parameters that describe how widely it distributes and how efficiently it is eliminated.

    • These concepts are quantified by the volume of distribution and clearance. Together, these factors determine a drug's half-life, a dependent parameter that define the drug' s duration of action and dosing frequency.

    • What follows establishes conceptual and mathematical frameworks for volume of distribution and drug half-life.

      • Volume of Distribution (V_d)

        • ​The volume of distribution, denoted as V_d , is a fundamental pharmacokinetic parameter providing a quantitative measure of a drug's distribution throughout the body's various compartments, either remaining within the plasma or moving into extravascular tissues. 

        • V_d  is defined as a proportionality constant that relates the total amount of drug present in the body at a specific time to the concentration of the drug measured in the plasma.

          • The volume of distribution is an apparent or hypothetical volume, not a literal one in physiological space.

            • This view is important in appreciating the extent of the drugs distribution.

          • Single-compartment pharmacokinetics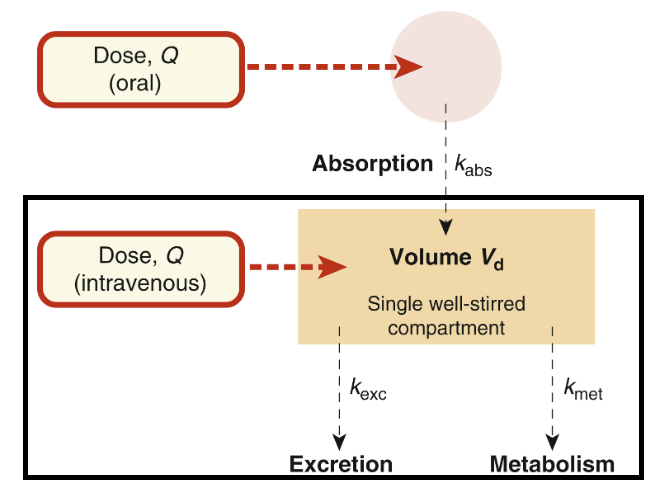

            Attribution: Corresponds to slight modification of Fgure 11.2 from (10); Applies when plasma concentration declines exponentially after drug administration. Ritter J Flower R Henderson G Loke Y MacEway D Robinson E Fullerton M Rang & Dale's Pharmacology Chapter 11 Pharmacokinetics Elsevier 2024

          • The equation for the volume of distribution is:

            • Volume of Distribution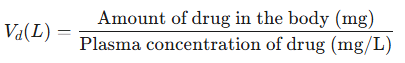

              Note that the equation describes Vd as an extrapolated value based on the ratio of the total dose administered and the resulting plasma drug level.5,6 The above equation refers to a model in which the body is viewed as the single homogeneous compartment. In this case, the one-compartment model considers that all drug administration directly enters the central compartment and furthermore, distribution of the drug occurs instantly throughout the volume, V.1 There are certain methods available to calculate the Vd of compartments. For example, consider a central, intravascular compartment. The method involves measuring drug levels in various times after intravenous drug administration. These measurements typically begin soon after administration. The approach requires calculation at time zero which can not be directly actually measured. What can be done is to estimate a volume referred to as Vinitial or Vc the first and typically rapid phase of distribution through the central compartment or Vd of the central component from the rapid distribution phase. Consider the graph below:

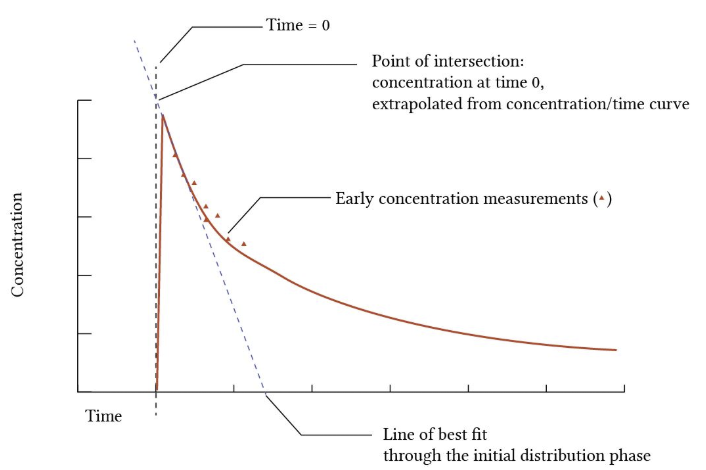
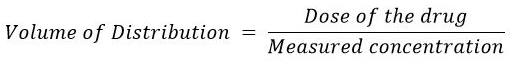
              Note the relationship between dose of the drug and measure concentration below: In the graph above note the triangles representing drug concentration at various time points after IV administration. The concentration at the first time point is somewhat after the drug is actually been administered IV.  However, they best fit line is computed defining the initial distribution phase and extrapolated back to time = 0. Since we know the dose of the drug and we have determined by this extrapolation method the apparent concentration at t = 0, the volume of distribution can be calculated using the above equation. With the dose of the drug expressed in mg and the measured drug concentrations expressed in mg/L, the ration gives the units of volume, L.

              Attribution:  For the graph above and description of the process to obtain the volume of distribution of the initial distribution phase.9 Yartsev A Volume of distribution. Last Updated December 18, 2023. Deranged Physiology https://derangedphysiology.com/main/cicm-primary-exam/pharmacokinetics/Chapter-202/volume-distribution

        • The term "apparent" is central critical to understanding this concept.

          • The volume of distribution does not represent a real anatomical volume.

            • For many drugs, the calculated V_d can can far exceed the total volume of body water (approximately 42 L in a 70 kg adult).

              • A drug with a V_d  of 500 L, for instance, is not distributing into 500 L of fluid.

                • Instead, this large value is a mathematical reflection of the drug's high affinity for tissues relative to its affinity for plasma.

                • When a drug binds extensively to components outside the plasma, such as proteins in muscle or lipids in adipose tissue, only a small fraction of the total drug in the body remains in the plasma to be measured.

                  • According to the equation, when the denominator (plasma concentration) is very small relative to the numerator (total amount of drug in the body), the resulting Vd must be very large to maintain the mathematical relationship.

                  • Therefore, V_d  ​is better understood not as a physical volume but as an index of partitioning, indicating the degree to which a drug is sequestered in extravascular tissues.

            • Drugs and their Apparent Volumes of Distribution⁷

              Drug	Apparent Vd in Liters
              Chloroquine	12950 L
              Digoxin	500 L
              Doxepin	1400 L
              Flurazepam	1540 L
              Haloperidol	1400 L
              Azithromycin	2170 L
              Amiodarone	4620 L

            • These values can be compared to volumes associated with the following compartments: Blood: 7 L Plasma: 4 L Whole body: 42 L

              For example, suppose a patient has taken 500 mg acetaminophen. So the amount of drug equals 500 mg. After about an hour, the concentration of blood in the plasma where blood = plasma + red blood cells are) is 8 ug/mL or 8 mg/L. Since we know that the volume of distribution for acetaminophen is about 50 L than the amount (one hour after dosing) = 8 mg/liter * 51 liter = 408 mg. So about 408 mg remain in the body given that 500 mg of drug was administered. Thus the volume of distribution as a proportionality factor which converts between amounts and concentration.8

              Looking at the drug table above, consider digoxin, with an apparent volume of distribution of 500 L. Digoxin preferentially is bound to specific receptors, the Na+/K+-ATPase in muscle and adipose tissue. Therefore, only limited amount of drug remains in the plasma to be measured. More generally, a small value for the volume V may suggest that the drug is maintained in the bloodstream, which may be therapeutically desirable (e.g. leukemia). Some newer drug formulations involve encapsulation in liposomes or nanoparticles that affect drug distribution. Therefore, V can change as result of binding to high-affinity receptors, plasma and tissue proteins, the partition coefficient of the drug in fact, concentration of the drug and poorly perfused tissues or encapsulation. Other factors for given drug that influence the volume of distribution include the patient's age, body composition, gender and the presence of disease.1

             

      • Interpreting V_d Values

        • The magnitude of the volume of distribution provides insight into a drug's physicochemical properties and its behavior in the body.

          • Low Volume of Distribution⁵

            • A drug with a low V_d (e.g., less than 15 L) demonstrates a propensity to remain primarily within the vascular compartment (plasma).

            • This V_d (< 15 L) is characteristic of drugs that are large molecules, are highly bound to plasma proteins like albumin, or are hydrophilic (water-soluble).

              • These properties restrict their ability to cross cell membranes and enter tissues.

                • Consequently, a lower dose of such a drug is required to achieve a desired therapeutic concentration in the plasma.

                • Warfarin is a classic example of a drug with a low V_d due to its extensive binding to plasma albumin.

          • High Volume of Distribution⁵

            • A drug with a high V_d (e.g., greater than 42 L) will moves from plasma and distribute widely into extravascular compartments, such as adipose tissue and intracellular fluid.

              • This behavior is typical of drugs that are lipophilic (fat-soluble), have low plasma protein binding, and/or exhibit high affinity for tissue binding sites.

              • Since a significant portion of the drug is sequestered in these tissues and not present in the plasma, a higher dose is required to achieve a given plasma concentration.

                • For example, chloroquine has a very large V_d (over 13,000 L) due to extensive binding to tissues like the liver, spleen, and melanin-containing cells.

      • Compartmental Models and V_d Calculation⁵

        • Dug distribution is frequently described using compartmental models, which model body's complex physiology as a series of interconnected compartments.

          • Single-Compartment Model^5,11

            • In the simplest model, the body is treated as a single, uniform compartment.

              • It is assumed that after administration, the drug distributes instantaneously and equilibrates throughout this entire volume.

              • For a drug following this model, a plot of the logarithm of plasma concentration versus time yields a straight line. The initial plasma concentration at time zero. See graph above.

          • Multi-Compartment Model^5,11

            • Most drugs exhibit more complex distribution patterns that are better described by multi-compartment models.

              • The most common is the two-compartment model, which divides the body into a "central" compartment and a "peripheral" compartment.

                • The central compartment consists of the plasma and highly perfused organs where the drug distributes rapidly, such as the liver, kidneys, and brain.

                • The peripheral compartment comprises tissues where the drug distributes more slowly, like muscle and fat.

                  • This model results in a biphasic decline in plasma concentration when plotted on a semi-logarithmic scale.

                    • There is an initial, rapid decline known as the distribution phase (alpha phase, t_1/2α ), representing the drug's movement from the central to the peripheral compartment.

                    • The distribution phase is followed by a slower, terminal decline known as the elimination phase (beta phase, t_1/2β ) which reflects the elimination of the drug from the central compartment after distribution equilibrium has been approached.

                    • Two-Compartment Model¹²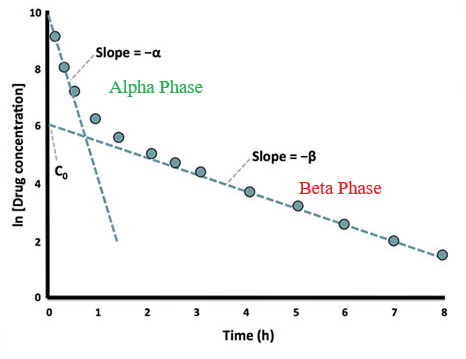

                      "Graph of plasma drug concentration (logarithmic scale) against time after intravenous dose. For drugs that are rapidly distributed into a single compartment from which they are subsequently eliminated the graph would contain a simple straight line slope. "The fact that this graph shows two slopes indicates there is a distribution phase as drug moves out into a second peripheral compartment before an equilibrium is reached throughout the whole volume of distribution. "At that point elimination occurs steadily from the central compartment.  "a and b are the rate constants of distribution and elimination respectively. C0 is the extrapolated concentration at time 0 that would've occurred if the drug had been instantaneously distributed in to its complete volume of distribution (Vd)."12  Attribution: The figure above is of slight modification of figure 2 from reference 12. The figure legend is from reference 12. Pharmacokinetics V. Two-compartment model. University of Aberdeen (2025). https://www.abdn.ac.uk/medical/elf/courses/view/144053/pharmacokinetics-v/1/page4#

           

          • Types of V_d ⁵

            • Reflecting these complex kinetics, several different values for the volume of distribution can be calculated.

              • These include:

                • Volume of the central compartment  (V_c),

                • Volume of distribution during the terminal elimination phase (V_dβ), and

                • Volume of distribution at steady state (V_ss).

                  • Of these, V_ss is generally considered the most clinically relevant parameter, as it represents the volume at a state of equilibrium between compartments and is used to determine the appropriate loading dose for a drug.⁵  

          • Factors Influencing Volume of Distribution

            • Volume of distribution is not a fixed property of a drug but is influenced by a combination of the drug's characteristics and the patient's physiology.

              • Drug Properties

                • Key physicochemical properties of the drug itself are major determinants.

                  • These include its molecular size, charge, acid dissociation constant (pKa), lipid-water partition coefficient (a measure of lipophilicity), and its affinity for binding to plasma proteins and tissue components.⁵

            • Patient Physiology and Pathophysiology

              • Body Fluid Status

                • Conditions that alter body fluid volumes, such as dehydration, edema, or ascites (a common complication of cirrhosis), can change the V_d of water-soluble drugs.

                  • For instance, the accumulation of ascitic fluid can greatly increase the V_d of highly water-soluble drugs, leading to lower than expected plasma concentrations.^9,13 

              • Plasma Protein Concentrations

                • Diseases like liver failure or malnutrition can lead to hypoalbuminemia (low plasma albumin), reducing the binding of acidic drugs and potentially increasing their V_d.¹³ 

              • Body Composition

                • Extremes of age, obesity, and pregnancy can alter the relative proportions of fat, water, and muscle, thereby affecting the distribution of drugs.

                  • For example, the V_d of lipophilic drugs is often increased in obese individuals due to the larger adipose tissue mass.¹⁴

              • Tissue Perfusion

                • Reduced blood flow to tissues, as seen in shock or heart failure, can decrease the rate and extent of drug distribution to peripheral compartments.¹⁵

      • Clinical Significance of Volume of Distribution

        • The primary clinical application of the volume of distribution is in the calculation of a loading dose.¹⁶ 

          • A loading dose is a larger-than-usual initial dose administered to rapidly achieve a target therapeutic plasma concentration, bypassing the time it would otherwise take to reach this level with smaller, repeated maintenance doses.⁵ 

          • The relationship is defined by the equation:

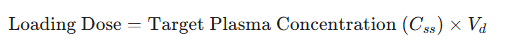
            • This equation demonstrates a direct and intuitive relationship: a drug that distributes widely into the tissues (high V_d) requires a proportionally larger loading dose to "fill" this large apparent volume and achieve the desired concentration in the plasma.²⁹

    • Drug Half-Life (t_1/2)

      • Definition:  The elimination half-life, symbolized as t_1/2, is a fundamental pharmacokinetic parameter defined as the time required for the amount of a drug in the body, or its concentration in the plasma, to be reduced by 50%. ²⁹

        •  It is a basic measure of how long a drug persists in the body after administration.

      • Kinetics of Elimination: The concept of half-life is most clearly applied to drugs that follow first-order elimination kinetics, which includes the vast majority of therapeutic agents at their usual doses.¹⁸

      • First-Order Kinetics: In a first-order process, a constant fraction or percentage of the drug is eliminated per unit of time.³⁰  

        • This means the rate of elimination is directly proportional to the drug concentration; the higher the concentration, the greater the amount of drug eliminated per unit time.

        • A key feature of first-order kinetics is that the half-life is constant and independent of the drug concentration.

      • Exponential Decay: The elimination process follows an exponential decay pattern.

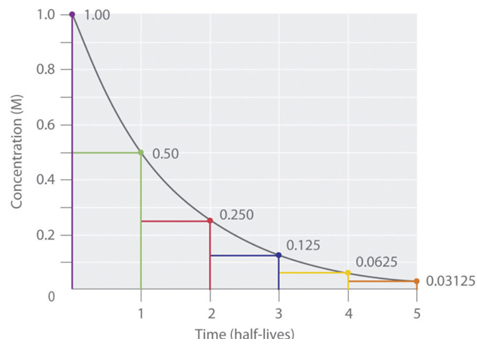
        • After one half-life, 50% of the initial drug amount remains.

        • After two half-lives, 25% remains (50% of 50%).

        • After three half-lives, 12.5% remains, and

        • After four half-lives, only 6.25% of the original dose is left.³¹

          • "Half-Life Elimination Curve. The have-life elimination of the drug is illustrated by an elimination curve, which plots the amount of drug remaining in the body over time. "Time is represented on the independent axes, whereas drug plasma concentration is represented on the dependent axes." Chemistry Libre Texts Attribution: Figure 1 from reference 31 Hallare J Gerriets Elimination Half-Life of Drugs. StatPearls. National Library of Medicine Bookshelf. (Last update: May 3, 2025).31  https://www.ncbi.nlm.nih.gov/books/NBK554498/

             

        • Time to Elimination: A drug is considered to be effectively and completely eliminated from the body after approximately four to five half-lives have passed, as by this point, 94% to 97% of the drug has been removed.

      • Extending Half-life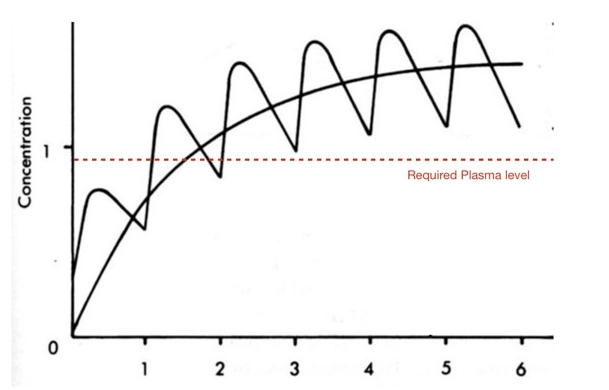

        "The half-life of the drug has major affect on both the size of the dose that is given in the frequency of dosing. "For a short-half-life drug where the clinical efficacy is limited by the trough levels of the drug it may require multiple repeated dosing to maintain drug levels above the required levels, in addition it may require high loading dose." Attribution: Half Life: Cambridge MedChem Consulting Last Updated April 26, 2018. https://www.cambridgemedchemconsulting.com/resources/ADME/halflife.html

      • Governing Equation and Determinants

        • A critical point of understanding is that half-life is not an independent physiological parameter.

          • Instead, it is a dependent or secondary parameter whose value is determined by the two primary parameters of drug disposition: volume of distribution (V_d) and clearance (CL).²⁹

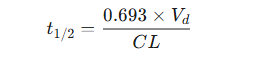
          • The constant 0.693 is an approximation of the natural logarithm of 2(ln(2)), which arises from the integration of the first-order rate equation and reflects the exponential nature of the elimination process.32

             

          • This equation reveals the direct and inverse relationships that govern half-life:

            • t_1/2 is directly proportional to the volume of distribution (V_d).³³ 

              • If a drug has a large volume of distribution, it is extensively sequestered in tissues, making it less available to the eliminating organs (like the liver and kidneys).

              • This protects the drug from elimination and thus prolongs its half-life.

            • t_1/2 is inversely proportional to clearance (CL).³³   

              • If the body's efficiency in eliminating the drug is high (high clearance), the drug will be removed more rapidly, resulting in a shorter half-life.

      • Factors Influencing Half-Life

        • Because half-life is dependent on V_d and CL, any physiological, pathological, or pharmacological factor that alters these primary parameters will consequently alter the half-life.³⁴

          • Examples affecting volume of distribution and therefore drug half-life include drug properties such as charge, protein binding, and lipid-water partition coefficients.

          • Other examples relate to pathophysiological conditions that patients may exhibit including obesity and edema.

            • Drug clearance and therefore half-life is dependent on active drug excretion, physiological status of organs involved in clearance, mainly kidneys and liver) and susceptibility to drug to metabolism often by the cytochrome P450 drug metabolizing system.³⁴

          • Factors that Increase Half-Life

            • Increased V_d : Conditions like obesity can increase the V_d for lipophilic drugs, prolonging their half-life. Similarly, fluid accumulation in edema or ascites increases the V_d for hydrophilic drugs.

            • Decreased V_d : Reduced V_d  is a common and clinically significant cause of prolonged half-life.

              • Renal disease reduces the clearance of renally excreted drugs, and hepatic disease (e.g., cirrhosis) reduces the clearance of hepatically metabolized drugs.

                • Drug interactions involving enzyme inhibitors also decrease clearance.³⁴

          • Factors that Decrease Half-Life

            • Decreased V_d : Reduction in drug tissue binding, for example, can reduce V_d .​

            • Increased CL: This can occur through the induction of metabolic enzymes by other drugs (e.g., rifampin inducing cytochrome P450 enzymes) or in certain physiological states like augmented renal clearance in some critically ill patients.³⁵

          • Half-life dependencies noted above underscores why a single published half-life value for a drug must be interpreted with caution.

            • The half-life in a healthy young adult may be drastically different from that in an elderly patient with renal impairment.²⁹ 

              • For example, in a patient with both renal failure and decreased muscle mass (a key binding site for digoxin), the clearance of digoxin is reduced, which acts to lengthen its half-life.

              • However, the volume of distribution is also reduced due to less tissue binding, which acts to shorten its half-life.

                • The net result is that the half-life of digoxin in such a patient is prolonged, but often less than would be predicted based solely on the change in renal function.

                • This example illustrates complex interplay between primary parameters in determining the observed half-life.²⁹

        • Clinical Significance of Drug Half-Life

          • Drug half-life is one of the most frequently used pharmacokinetic parameters in clinical practice due to its direct implications for designing a safe and effective dosing regimen.

            • Determining the Dosing Interval (τ): Half-life is the primary guide for deciding how often a drug should be administered.

              • Drugs with short half-lives need to be given more frequently to maintain concentrations within the therapeutic window, whereas drugs with long half-lives can be dosed less often, such as once daily.³²

            • Predicting Time to Steady State: The time required to reach a steady-state concentration with a regular, repeated dosing regimen is determined by the half-life.

              • As noted previously, it takes approximately four to five half-lives to reach about 97% of the final steady-state level.

              • This principle is crucial for patient education and for evaluating the therapeutic effect of a newly initiated medication.³⁶

            • Estimating the Duration of Action: Half-life provides a useful estimate of how long a drug's pharmacological effect will persist after a single dose is given or after a chronic regimen is stopped.³⁷

            • Guiding Washout Periods: When switching from one medication to another, particularly if there is a risk of interaction, the half-life dictates the necessary washout period to ensure the first drug has been adequately eliminated from the body.

          • For drugs that follow multi-compartment kinetics, it is important to distinguish between the distribution half-life (t_1/2α) and the elimination half-life (t_1/2β).⁵

            • The initial rapid decline in plasma concentration is governed by the distribution of the drug from the central to peripheral compartments.

              • The termination of the clinical effect of some drugs is due to this rapid redistribution, not elimination.

                • A classic example is the intravenous anesthetic thiopental.

                  • Its anesthetic effect is very brief because the drug rapidly redistributes from the brain (central compartment) into adipose tissue (peripheral compartment).

                    • This occurs over a short distribution half-life.

                  • However, its elimination half-life, which describes the slow release of the drug from fat and its subsequent metabolism, is much longer.

                    • Relying solely on the elimination half-life in this case would be highly misleading for predicting the duration of anesthesia.³⁸

  • Drug Clearance

    • Drug clearance (CL) is the pharmacokinetic parameter that quantifies the efficiency of the body's processes for irreversible drug elimination.¹⁷  

      • Clearance is conceptually defined as the theoretical volume of plasma (or blood) that is completely cleared of a drug per unit of time.

        • The standard units for clearance are volume per time, such as liters per hour (L/hr) or milliliters per minute (mL/min).

        • It is important to distinguish clearance from the rate of elimination; clearance is a measure of volume cleared, while the rate of elimination is the mass of drug removed per unit time (e.g., mg/hr).¹⁷  

      • Rate of Elimination of Drug (mass/time) = Clearance (volume/time) * Plasma Drug Concentration (mass/volume)¹⁸

        • This equation shows that for a drug following first-order kinetics, where clearance is a constant, the rate of elimination is directly proportional to the drug's plasma concentration.

          •  As the plasma concentration falls, the rate of elimination decreases, but the clearance—the fractional volume being cleared—remains the same.

      • The body eliminates drugs via multiple organs, primarily the liver and the kidneys. Total body clearance, also known as systemic clearance (CL_T) is therefore the sum of the clearances from all individual eliminating organs. This additive nature is expressed as:

        • Total Clearance: some of clearances from all eliminating organs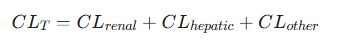

           

          • For most drugs, the contribution from "other" routes, such as pulmonary excretion for volatile anesthetics or excretion into sweat or saliva, is minor.

            • Total clearance is predominantly a function of renal and hepatic clearance.

      • A model-independent method for calculating total clearance involves using data from an intravenous dose.

        • After IV administration, the total clearance can be determined from the administered dose and the total drug exposure over time, which is quantified by the area under the plasma concentration-time curve from time zero to infinity. (AUC)_0-∞ .

          •  

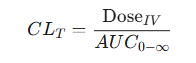
          • The above equation is fundamental in pharmacokinetic analysis because it allows determination of a fundamental physiological parameter from empirical plasma concentration data.^19,20

  • Hepatic Clearance (CL_h)

    • Hepatic clearance (CL_h) quantifies the irreversible removal of a drug from the body by the liver.

      • This process is the result of two primary mechanisms:

        • Hepatic metabolism (biotransformation of the parent drug into metabolites by liver enzymes) and

        • Biliary excretion (secretion of the drug or its metabolites into the bile).²¹

    • Determinants of Hepatic Clearance: Three primary physiological factors²²

      • Hepatic Blood Flow (Q_H), Representing the rate of drug delivery to the liver. This rate is about 1.5 L/min or 90 L/hour in a healthy adult.

      • Fraction Unbound (f_u): Only the fraction of the drug in the plasma that is not bound to proteins (like albumin) is generally considered free to cross hepatocyte membranes and be metabolized.

      • Intrinsic Clearance (CL_int): This term describes the inherent, maximum capacity of the liver's enzymatic systems to metabolize a drug, independent of any limitations imposed by blood flow or protein binding.  It reflects the intrinsic activity of enzymes like the cytochrome P450 (CYP) family and is analogous to the V_max/K_m ratio from Michaelis-Menten enzyme kinetics.

      • Hepatic Clearance

        Attribution Figure on Hepatic clearance, slightly modified from reference 22. Yartsev A Hepatic Clearance. Last updated December 18, 2023. Deranged Physiology. https://derangedphysiology.com/main/cicm-primary-exam/pharmacokinetics/Chapter-3336/hepatic-clearance

     

    • Hepatic Extraction Ratio (E)

      • The above factors are the basis of the hepatic extraction ratio (E).

        • The extraction ratio is the fraction of the drug that is removed from the blood during a single pass through the liver.

          • It is a dimensionless value ranging from 0 (no drug extracted) to 1 (100% of the drug is extracted).

          • Hepatic clearance can then be elegantly expressed as the product of liver blood flow and the extraction ratio:²²

          • Hepatic Drug Clearance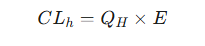

            This equation illustrates that hepatic clearance is determined by two factors: (1) the rate at which the drug is delivered to the liver (QH) and (2) the efficiency with which the liver removes the drug (E).21

     

    • Drug Classification Based on Extraction Ratios

      • The interplay between Q_H, f_u and CL_int determines the extraction ratio, and this allows for a clinically powerful classification of drugs into two main categories, which predicts their behavior in different clinical scenarios, that is High-Extraction Drugs and Low-Extraction Drugs.

        • High-Extraction Drugs (E > 0.7)²³

          • For these drugs, the intrinsic clearance (CL_int) is very high, meaning the liver's metabolic capacity is so great that it can remove the drug much faster than it is delivered.

            • Therefore, the rate-limiting step for elimination is the delivery of the drug to the liver via blood flow.

              • Examples of drugs that exhibit flow dependent hepatic clearance (high hepatic extraction ratio) include:

                • Morphine, Lidocaine, Verapamil, Nitroglycerin, Propranalol

          • Flow-Dependent Clearance

            • The clearance of high-extraction drugs is primarily dependent on hepatic blood flow. The equation for clearance simplifies to:

              • CL_h ≈ Q_H ²⁴

          • Clinical Implications

            • The clearance of these drugs is sensitive to conditions that alter hepatic blood flow.

              • For example, in patients with congestive heart failure, reduced cardiac output leads to decreased Q_H and therefore decreased clearance, resulting in higher plasma concentrations and an increased risk of toxicity.

              • Drugs that reduce hepatic blood flow (e.g., propranolol, a β-blocker) can decrease their own clearance.²⁵

                • Protein binding has little effect on the clearance of high-extraction drugs, as the liver's high metabolic capacity can efficiently remove the drug from binding proteins as it passes through.

            • Certain disease states alter blood flow and therefore would be expected to change clearance of certain drugs.^22,26

              • Early sepsis in which hepatic arterial blood flow may double.

              • Late sepsis in which hepatic blood flow and flow to other organs is dramatically decreased.

              • Hemorrhagic shock with associated hypovolemia and hemorrhage reduces liver blood flow accordingly. In this circumstance, drug half-life may be notably increased.

              • Cardiogenic shock with associated reduction in cardiac output and peripheral vasoconstriction results in significant hepatic blood flow reduction.^22,26

        • Low-Extraction Drugs (E < 0.3)

          • For these drugs, the intrinsic clearance (CL_int) is low compared to hepatic blood flow.

            • The liver's metabolic capacity is the rate-limiting step, not the rate of drug delivery.²²

          • Capacity-Limited and Binding-Sensitive Clearance

            • The clearance of low-extraction drugs is largely independent of hepatic blood flow. Instead, it is dependent on the fraction of unbound drug and the intrinsic clearance.

            • The equation simplifies to: CL_h ≈ f_u * CL_int.

          • Clinical Implications

            • The clearance of low extraction drugs is sensitive to factors that alter enzyme activity (induction or inhibition) or plasma protein binding.

              • Co-administration of a CYP enzyme inducer (like rifampin) will both increase the drugs metabolism, increase CL_int and thus increase the clearance of a low-extraction drug, potentially leading to therapeutic failure.²⁷ 

              • An enzyme inhibitor, by contrast, will decrease clearance and increase the risk of toxicity.²⁷ 

              • Changes in protein binding (e.g., displacement by another drug or hypoalbuminemia in liver disease) will also alter the clearance of these drugs.²⁸ 

                • This is known as restrictive clearance, as only the free, unbound drug is available for metabolism.

          • Examples of low-extraction drugs: warfarin, phenytoin, diazepam, and theophylline.

        • Classification of Low-Extraction and High-Extraction Drugs and Drug-Protein Binding

          • A particularly non-intuitive consequence of this framework relates to protein binding displacement.

            • When a second drug displaces a primary drug from its binding sites on plasma proteins, the unbound fraction (f_u) of the primary drug increases.

            • For a low-extraction (restrictively cleared) drug, where CL_h ≈ f_u * CL_int  , the increase in f_u leads to a proportional increase in hepatic clearance.

              • The net effect is that the steady-state concentration of free drug, which is responsible for the therapeutic effect, remains largely unchanged, minimizing the risk of toxicity.

              • In contrast, for a high-extraction (non-restrictively cleared) drug, where CL_h ≈ Q_H , clearance is independent of protein binding.

                • Therefore, an increase in f_u does not change the total clearance.

                • However, since a larger fraction of the total drug in the body is now free, the steady-state concentration of free drug increases significantly, posing a major risk of toxicity.

                • This reveals a critical principle: for predicting the clinical outcome of protein-binding drug interactions, understanding the drug's extraction ratio is more important than simply knowing its degree of protein binding.